Duplicate a PIN Digit to Increase Obfuscation

Let's say you are setting up a PIN code to secure access to your bank account at an ATM. When you walk up to the ATM, you punch in your four digit PIN and the machine allows you to withdraw money. Now let's assume there is some nefarious thief who steps up to the machine after you have left. Due to your Cheeto-covered fingertips, the thief can identify which buttons you had pressed on the PIN pad, but not the order in which they were pressed.

The question I had is this: is it better to have a PIN composed of four unique digits, or is it better to duplicate one or more of them? And by better here I mean to ask whether a thief has more or fewer potential possibilities to try via a brute-force strategy. If only one button is covered in Cheeto dust, then the thief knows the password must be N repetitions of that number, where N is the length of the PIN passcode, but things get more complicated with more revealed digits and longer passwords.

The Brute-Force Crunch

Here I wrote a simple python script that iterates through all possible PINs of a given length and measures the unique number of digits in each code. Then, I evaluate how many unique PINs could potentially satisfy a given query. In the figure below, I tabulated the total counts of PINs as a function of both the number of revealed digits and the length of the PIN.

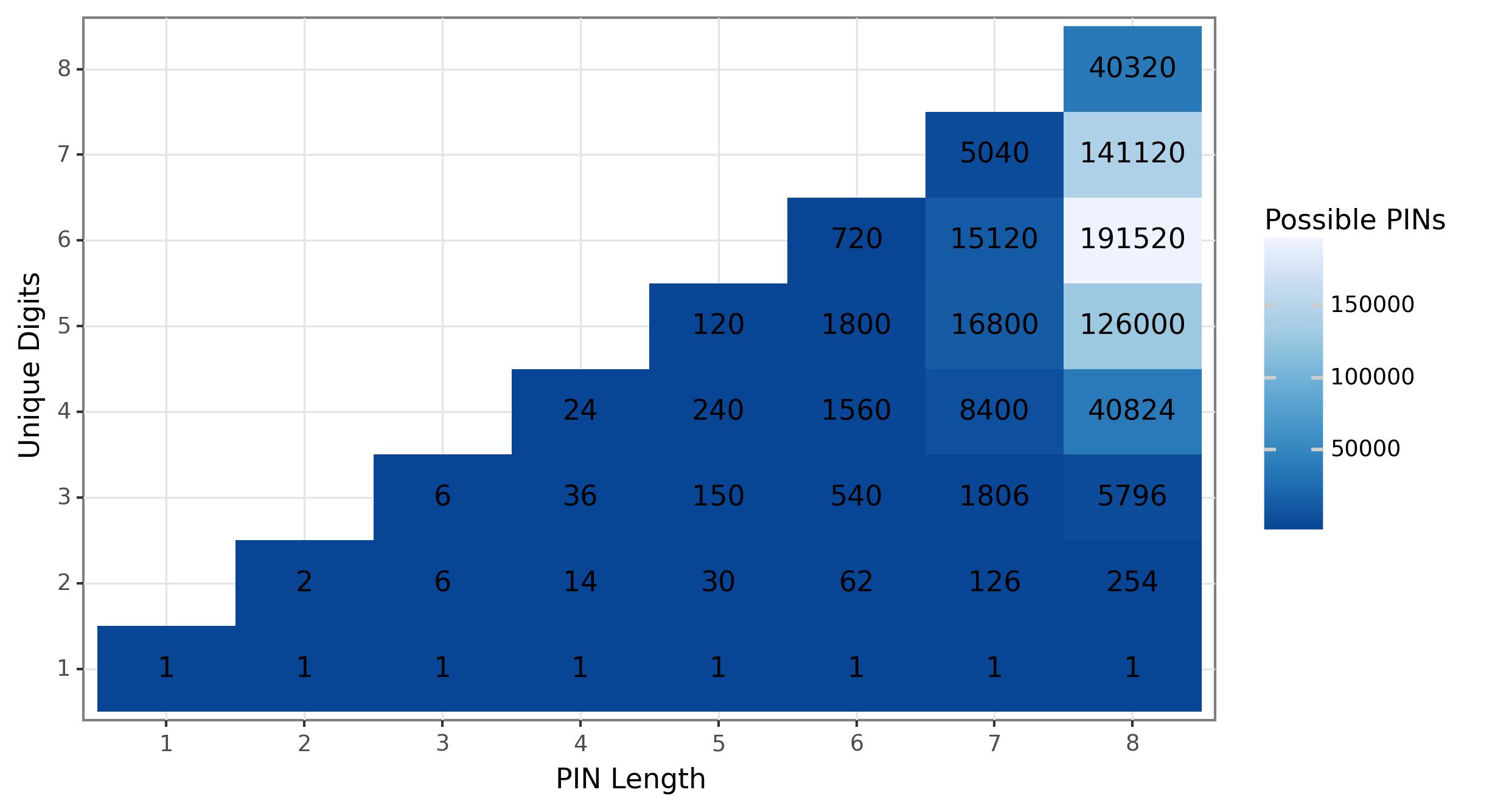Unique PINs that satisfy a revealed subset of digits.

Observations

Interestingly, it does seem that in this example, duplicating one digit in a 4-digit PIN seems to provide more obfuscation than using four unique digits. Further, as PINs get longer, the degree of obfuscation seems to change such that when considering an 8-long PIN, it appears to be beneficial to include two duplicated digits, revealing only 6 unique digits to some thief.

Finding a General Solution

I spent some time trying to get my head around a closed-form algebra describing this table, but got myself stuck. A few high-level observations to get anyone else started. I'd love to see if someone more well-versed in combinatorics has an equation that yields the values in the table above.

1. The diagonal is just the factorial sequence $$ n_{i} = i! $$
2. The second diagonal is the product of the index factorial and the nth triangle number $$n_{i} = i! * \Big(\frac{i^2+i}{2}\Big)$$
3. And that's about it. I'm pretty sure I'm close but can't figure out the terms for the inner diagnonal sequences.

Anyway, enjoy an interesting Sunday problem that I'll leave incomplete as an exercise to the reader.